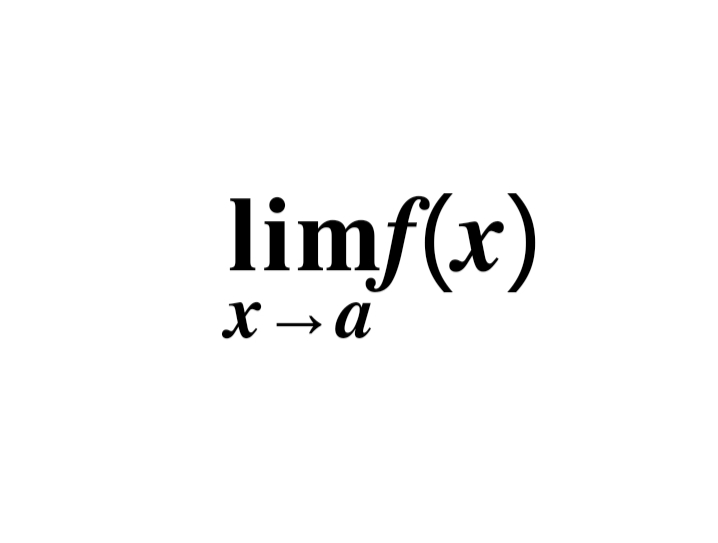লিমিট পড়ার আগে তাহলে আমাদের জানতে হবে লিমিট আসলে কি? তো দেখো গণিতে আমরা অনেক ধরনের প্রবলেম সলভ করে থাকি যেখানে আমাদের দেখা যায় কোন নির্দিষ্ট মানের জন্য টির মান পাওয়া যায় না। যেমন তুমি নিচের ফাংশন টি খেয়াল করো :
$$\frac{x^2-4}{x-2}$$
যদি x=2 বসানো হয় তাহলে ফাংশনটির আউটপুট অসংজ্ঞায়িত হয়। এরকমভাবে গণিতে অনেক ফাংশন আছে যেগুলার ফাংশনাল বিহেভিয়ার জানার জন্য এমন কোন বিন্দু থাকবে যে বিন্দু গুলার জন্য আমরা ফাংশনের কোন মান পাবনা সেক্ষেত্রে ওই মানগুলো জানার জন্য বা এখানে বলতে পারো আন্দাজ করার জন্য যে মানগুলো কি হতে পারে- এ সকল স্টেজে তুমি লিমিট ব্যবহার করে খুব সহজেই ওই মানটা সম্পর্কে অবগত হতে পারো। যেমন তুমি দেখো উক্ত ফাংশনে 2 বসালে ফাংশনটি অসংজ্ঞায়িত হলেও দুয়ের জন্য যে ফাংশনের মান হয় সেটা কিন্তু তুমি খুব সহজে আন্দাজ করতে পারলে। আরেকটু ভালোভাবে বোঝার জন্য নিচের চিত্রটি খেয়াল করো:
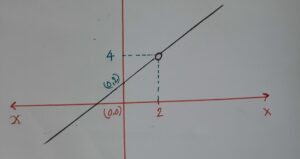
এবার নিচের ফাংশন টি খেয়াল করো :
$$\frac x{\sin x}$$
তোমাকে যদি বলা হয় যে এই ফাংশনের x= 0 বিন্দুতে ফাংশনটির মান কত তুমি বের করতে পারবে হ্যাঁ পারবে কি আসবে 0/0 । এইটা আসলে কোন উত্তর হলো না এটা অসংজ্ঞায়িত তাই না? যদি তাই হয়, তাহলে নিচের গ্রাফটি খেয়াল করো:
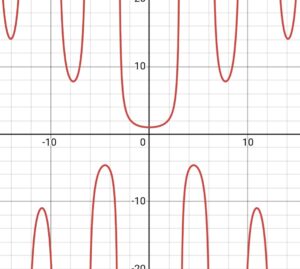
কি দেখলে মান আসে না? উত্তর হলো, হ্যাঁ ওখানে অসংজ্ঞায়িত মানটি জানা থাকার কারণে তুমি ফাংশনটির সম্পূর্ণ গ্রাফটি পেলে। মানে এটির আচরন কেমন বুঝতে পারলে, তাই না? গ্রাফটি প্যারাবোলিক এখন তাই তো? তাইলে মানটি বের করবো কিভাবে?
এই সলিউশনটা আনার জন্যই লিমিট পড়তে হবে বুঝতে পারলে? তারমানে যে ফাংশনে কোন চলক এক্সাক্ট মানের জন্য ফাংশনটি ফাংশনটির মান বের করা সম্ভব না হলেও tends to বা close to এর জন্য আমরা ফাংশনটির মান বের করতে পারি এই জাতীয় পড়াশোনাই হচ্ছে লিমিটের অন্তর্ভুক্ত তাহলে বুঝতে পারলে লিমিট কেন পড়তে হবে?