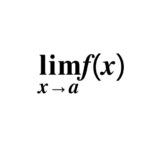ব্লগটি পড়া শুরু করার পূর্বে মাইন্ড সেট করে নাও যে আসলে তুমি কি পড়তে যাচ্ছো। দেখো পড়াশুনা ভালো পাড়া বা বোঝার একটা বড় ব্যপার হলো তুমি আসলে কি জানতে চাও সে সম্পর্কে ভালোভাবে অবগত হওয়া, নইলে দেখবা আর্টিকেল টা পড়েও দিনশেষে তুমি আসলে কিছুই বুঝতে পারো নি।
এখানে আমরা জানবো যে:
1/0 কি আসলেই ইনফিনিটি বা অসীম?
মানে ;$$\frac10=\infty$$
এবার নিচের দুটি সমীকরন দিকে খেয়াল করো :
$$\frac1{0^+}\rightarrow\infty\\\frac1{0^-}\rightarrow-\infty$$
এগুলোকে এভাবে পড়া হয় (1/0+) tends to positive infinity.
(1/0-) tends to negative Infinity.
তাইলে আমাদের মটিভটা জেনে নেওয়া যাক, সেটা হলো যদি এরা অসীমের সংজ্ঞায় পরে যায় তাইলে এরা অসীম বা ইনফিনিটি আর যদি না যায় তো অসীম হবে না। এই জিনিসটাই আমরা এখানে ব্যখ্যা করার চেষ্টা করবো।
ইনফিনিটি আসলে কি?
সাধারন ভাবে ইনফিনিটি হলো খুবই বড় একটা সংখ্যা মান, মানে তোমার মাথায় এখন যে সংখ্যা মাথায় আসছে তার চেয়ে বড় মান।
আরও বড় মান চিন্তা করো কিন্তু তুমি তাও ইনফিনিটিকে ধরতে পারবে না। এটি আরও বড় হয়ে যাবে।
তার মানে তুমি একটা বিষয় বুঝতে পারতেছো কি যে ইনফিনিটি তোমার চিন্তার সাথে সাথে পরিবর্তন হচ্ছে তাই না?
তাইলে ইনফিনিটির সংজ্ঞা এভাবে দেওয়া যেতে পারে যে এটা একটা শুধু symbol কোন মান নয়, কিন্তু একটা চলক যা সময়ের সাথে সাথে পরিবর্তন হয়। ঐ যে বললাম তোমার চিন্তার সাথে সাথে পরিবর্তন হচ্ছে। তার মানে এটা কোন ফিক্সড সংখ্যা নয়। চলো গানিতিক ভাবে এটা দেখি:
$$\frac11=1\\\frac1{0.01}=100\\\frac1{0.00001}=10^5$$
তুৃমি দেখো যে 1 এর নিচে যত ছোট সংখ্যা তুমি আনতেছো তত বড় আউটপুট তুমি পাচ্ছো তাই না? অনুরূপ তুমি নেগেটিভ সংখার জন্যও সেইম পাবা সেক্ষেত্রে এটি নেগেটিভ দিকে বাড়তে থাকবে।
তো এমন অনেক অনেক ছোট সংখ্যা তুমি দাও যেমন ধরো দশমিকের পরে ৫ কোটি শূন্য তারপর 1, তাইলে তুৃমি এমন সংখ্যা পাবা তা আসলে এক্সপ্লেইন করা যাবে না মানে তোমার নিকট পেপার পেনসিল দিয়ে অন্তত লেখা কষ্টকর হবে। এটা তোমার নিকট এখন ইনফিনিটি। ধরো কোনো কারণে তুমি লিখেও ফেললা তখন ইনফিনিটি এর থেকে বড় সংখ্যা হয়ে যাবে। ঐ যে বললাম সময়ের সাথে সাথে পরিবর্তন হয়।
এবার চলো আলোচনা করা যাক tents to বা close to সম্পর্কে কারণ উক্ত জিনিসগুলা ক্লিয়ারলি জানার জন্য আমাদের এ বিষয়েও জানা থাকতে হবে। তো চলো শিখে ফেলি।
নিচের দুটি সমীকরন খেয়াল করো:
যখন তুমি x tends to 2 এবং x equal to 2 দেখলে, কি মাথায় আসলো?
যে একটা জায়গায় x কাছাকাছি মানে আছে আরেকটা জায়গায় নেই এইতো? তাই না?
ওকে বিষয়টি ঠিক তাই যখন x tends to 2 লিখা হবে তখন আসলে x এর মান two নয় এর কাছাকাছি কোন মান। আচ্ছা এর আবার দুইটা কেস হতে পারে:
তুমি 2 এর নিকট 1.8, 1.9, 1.99, 1.9999, 1.99999…. এভাবে যেতে পারো । আবার 2.01, 2.001, 2.00001….. এভাবে 2 এর নিকটে যেতে পারো।
চলো আমাদের একটা কমন ভুল দেখি যখন আমাদের কাছে কোন সংখ্যা আসে যা অনেক বড় বা ( সামথিং/০) আসে তখন আমরা খুব সহজে x=$ লিখে দিই। চিন্তা করো আমরা যে ডেফিনিশন শিখলাম এর সাথে আদও এটি যায় কি? উত্তর হলো একেবারেই না। তোমারে বলা হইলো যে এটা সময়ের সাথে সাথে।পরিবর্তন হবে। তুমি এক্সাক্টলি বলতে পারবে না যে ইনফিনিটি আসলে কত বড় মান। তাইলে তুৃমি এর আশে পাশে থাকতে পারো, তাই না? তাইলে কেউ এক্সাক্টলি ১/০ বা যাই ১/০ বা ৬/০ লিখুক ইনফিনিটিকে এক্সাক্টলি ডিফাইন করা অসম্ভব। তো তুমি কাছাকাছি যেতে পারো
এজন্য;
$$\frac1{0^+}\rightarrow\infty\\\frac1{0^-}\rightarrow-\infty$$
এগুলা ঠিক কিন্তু ১/০ এটা ভুল।
বলা যেতে পারে;
$$\frac10\neq\infty$$