ইলেকট্রন আবিষ্কার: থমসনের ক্যাথড রে পরীক্ষা

Read Time:11 Minute, 16 Second

ইলেকট্রন আবিস্কার রসায়ন জগৎ কে সুক্ষ্ণভাবে জানার পথ সুগম করে দেয়। দ্বার খুলে যায় কোয়ান্টাম ফিজিক্স নামক অধ্যায়ের। অন্যদিকে আবিষ্কার হওয়া প্রোটন ও নিউট্রন। ফলে পরমাণু যে অভিভাজ্য সেই নীতি আর টিকল না। একে রাদারফোর্ড, বোর এটোমিক মডেল সহ আরও বিখ্যাত থিওরি দিয়ে এটম বা পরমাণুকে বোঝার জন্য বিজ্ঞানীগন চেষ্টা চালাতে থাকেন যার ফলে আজ আমরা এই রসায়ন এতোটা ব্যাপকভাবে জানতে পারতেছি।

যাই হোক এটাকে বলা হয় জে. জে. থমসন ক্যাথড রে এক্সপেরিমেন্ট যার ফলে আসলে ইলেক্ট্রন আবিষ্কার হয় প্রকৃতপক্ষে।

যারা ইন্টারমিডিয়েট লেভেল আছো- মজার বেপার হলো তোমরা না জেনেই এই এক্সপেরিমেন্ট ব্যবহার পূর্বক তুমি ফিজিক্স এ বেশ কয়েকটি সমস্যা সমাধান করে থাকো। যেমন এই লিংকে।

তো আমরা ইলেক্ট্রন কিভাবে আবিষ্কার হয় তা জানবো।

জে. জে থমসন আসলে e/m এর মান বের করেছিলেন। যেহেতু চার্জের মান এর পূর্বেই বের করা হয়েছিল মিলিকানের তৈলবিন্দু পরীক্ষার মাধ্যমে।

তো চলো e/m এর মান বের করা যাক :
এজন্য যা লাগবে:
১. ক্যাথড রে
ক্যাথোড রশ্মি বা ইলেক্ট্রন রশ্মি (ই-বিম) হল ডিসচার্জ টিউবে পরিলক্ষিত ইলেকট্রনের প্রবাহ । যদি একটি খালি করা গ্লাস টিউব দুটি ইলেক্ট্রোড দিয়ে সজ্জিত করা হয় এবং একটি ভোল্টেজ প্রয়োগ করা হয়, ক্যাথোড থেকে নির্গত ইলেকট্রন (ভোল্টেজ সরবরাহের নেগেটিভ টার্মিনালের সাথে সংযুক্ত ইলেক্ট্রোড) এর কারণে ধনাত্মক ইলেক্ট্রোডের পিছনের গ্লাসটি জ্বলতে দেখা যায়।

এখানে key points দেখো-
উচ্চ ভোল্টেজ ডিভারেন্স প্রয়োগ করার করার অর্থ হলো ইলেক্ট্রন নিম্ন বিভব হতে উচ্চ বিভবে
গমন করবে। কেন ইলেক্ট্রন নেগেটিভ বিম হতে মুক্ত হয়ে পজেটিভ বিম এ গিয়ে আঘাত করে পদার্থ বিজ্ঞান বিষয়ে জানবো।
আচ্ছা তাইলে ক্যাথড রে পাওয়া গেল তাই না ?

২. তড়িৎ ক্ষেত্র প্রাবল্য (electric field Intensity): তড়িৎ ক্ষেত্রের কোন বিন্দুতে একটি একক চার্জ স্থাপন করলে সেটি যে বল অনুভব করে তাই তড়িৎ ক্ষেত্র প্রাবল্য এটা তো জানো?

চিত্রটি খেয়াল করো দেখো আসলে তড়িৎক্ষেত্র কোন চার্জের ওপট বল কিভাবে কাজ করে;

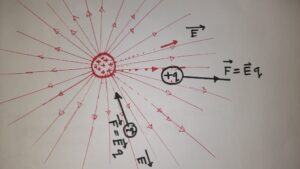
দেখো দুটি চার্জ প্লেট আছে তাইলে অবশ্যই তদের মাঝে একটা তড়িৎক্ষেত্র থাকবে, আর এর দিক হবে ধনাত্মক হতে ঋণাত্নক এর দিকে।
এবার তুমি একটা ধনাত্মক চার্জ q দাও, দেখবে চার্জটি যেদিকে তড়িৎক্ষেত্র ঐদিকে বল অনুভব করছে। বিষয়টি আরেক ভাবেও ব্যাখ্যা করা যায় যেমন : q চার্জটি ধনাত্মক বলে ধনাত্নক প্রান্ত বিকর্ষণ ও ঋনাত্নক প্রান্ত কে আকর্ষন করে তাইলে এটা লব্ধি তড়িৎ ক্ষেত্র ঋনাত্নক প্রান্ত যেদিকে ঐদিকে হলো।

আবার ঋনাত্নক চার্জ (-q) দাও দেখবো তার উল্টো দিকে বল অনুভব করবে।
তাহলে এ বিষয়টি পরিষ্কার হলো, তাই না?

যদি বুঝে থাকো তো চলো মূল বিষয়টির সমাধান করা যাক।

যখন ক্যাথড রে টিউবের মধ্যে দিয়ে গমন করে তখন এর ওপর একটা ইলেক্ট্রিক ফিল্ড দেওয়া হয় যার দরুন এটা বেকে যায়। কেন বেকে যায় বুঝতে পারলে?
কারন হলো ঐ যে চার্জ পার্টকেল যদি তড়িং ক্ষেত্রে গমন করে তাহলে বল (F=qE) অনুভব করবে। কারণ তড়িৎক্ষেত্র প্রাবল্যের সংজ্ঞা তেই বুঝতে পারছো আশা করি।

আচ্ছা একটু চিন্তা করো তো থমসন কেন তড়িৎক্ষেত্র নিয়ে আসলেন?
ব্যাখ্যাটি এভাবে দেওয়া যেতে পারে
আসলে ওনার চিন্তা হয়তো ছিলো ভর বের করা, তাইলে যদি বল আসে তাইলে অবশ্যই ভর চলে আসবে কারণ F=ma.

তাইলে,
$$F=ma$$
সুতরাং
$$F=qE=eE$$ যেহেতু q=e
$$ma= qE$$
$$a_y=\frac{Eq}{m_e}$$

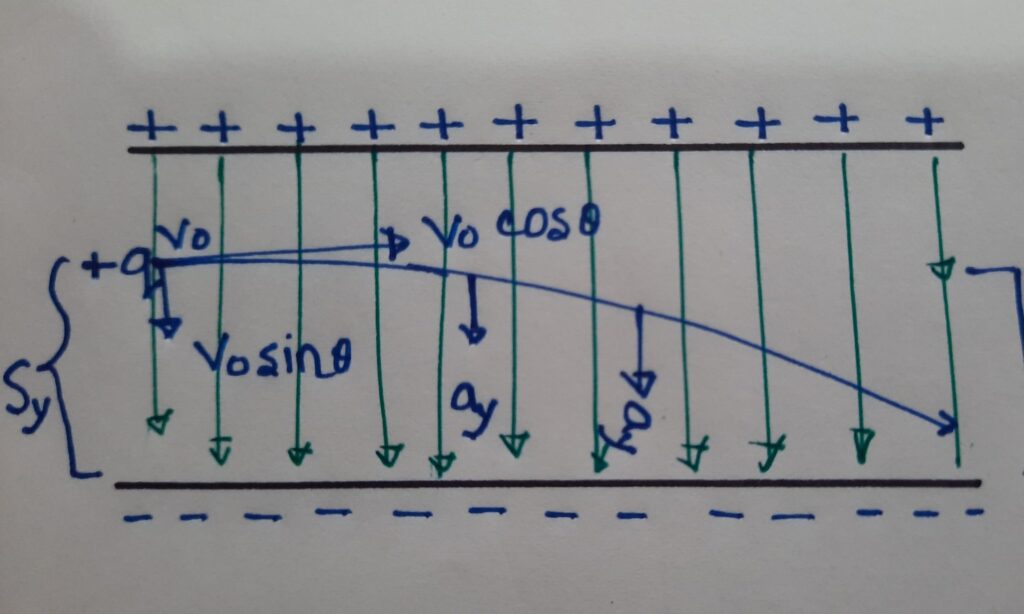
দেখো, ইলেক্ট্রনের গতিপথ টা কিন্তু প্রাসের মতো হয়ে গেছে তাইলে আমাদের প্রয়োজনীয় ক্যালকুলেশন এর কনসেপ্ট ব্যবহার করবো।

$$S_y=V_{0y}t+\frac12a_yt^2…………..(1.1)$$
Sy= y অক্ষের দিকে অতিক্রান্ত দুরত্ব; Voy = হলো y অক্ষের দিকে বেগের উপাংশ ।

এখানে Sy মানে হলো উলম্ব বরাবর কতটুকু দুরত্ব অতিক্রম করলো। আর এটা জানা থাকার কথা যে বস্তু যদি উলম্বতলে ( উপরের দিকে অথবা নিচের দিকে গমন করে) তাইলে সেইদিকে সকল জানা মানগুলোকে এনে যে চলকের মান বের করতে বলা হয় তা বের করবে।

তো চলো প্রাস(projectile motion) নিয়ে একটু বলা যাক
তুমি যদি (Figure 2.1) খেয়াল করে থাকো তাইলে দেখবে যে, বেগ এর মান যার উপাংশ লম্ব দিকে নেওয়া হয়েছে। আর এ জন্য লম্ব দিকে এর মান শূণ্য কারণ কোণের মান ০। ত্বরণের মানও কিন্তু Y অক্ষের দিকে নিবো তাই না? ঐ যে বললাম যেদিকে ক্যালকুলেশন ঐ দিকে সব মানকে নিতে হব। চিত্র খেয়াল করো (Figure 2.1).

এখন আমাদের Y অক্ষে Vo এর উপাংশ খুঁজে বের করতে হবে এবং এটি VoSinθ। যেহেতু θ শূন্য ডিগ্রি তাই কোন উল্লম্ব প্রাথমিক বেগ নেই।

আরেকটা কথা প্রাসের ক্ষেত্রে তুমি ত্বরণ g ব্যবহার করতে। কিন্তু, এখানে এই ত্বরণ ay সম্পর্কে তুমি কী ভাবো? উত্তর টা হলো এখানে একের অধিক বল আছে তো Fnet = ma হবে সেক্ষেত্রে ay ত্বরণ কাজ করবে। এটা কিন্তু নিউটনের দ্বিতীয় সূত্র। বিস্তারিত জানতে click here.

বিঃদ্রঃ:

এতক্ষণ পড়তে পড়তে হয়তে তোমার মনে প্রশ্ন আসতে পারে যে তাইলে থমসন F= mg আসবে এরকম একটা সেটআপ করে খুব সহজে বের করতে পারেন এতো কঠিনে যাওয়ার করণ কি?

এর একাধিক কারণ রয়েছে:

1) এটি অত্যন্ত ছোট ! এত অল্প ভরের কারণে, একটি ইলেক্ট্রনের উপর কাজ করে মহাকর্ষীয় বল হল নগণ্য। উদাহরণস্বরূপ, ইলেক্ট্রনের বিশুদ্ধ ভর এতই নগণ্য যে কোনও সুনির্দিষ্ট পরিমাপ করা প্রায় অসম্ভব।

2) থমসন যে ধরণের পরীক্ষা চালিয়েছিলেন। বিখ্যাত ক্যাথোড রে টিউব পরীক্ষায় তিনি বৈদ্যুতিক এবং চৌম্বক ক্ষেত্র ব্যবহার করেছিলেন। সুতরাং, তার ভর m এবং ইলেকট্রন চার্জ q এর অনুপাত ছিল।

আচ্ছা চলো পরের অংশে যাওয়া যাক – দেখো আমরা প্রায় সমাধানের দ্বারপ্রান্তে। তাই ধৈর্য ধরে একটু খেয়াল করলে সবই বুঝতে পারবে। আর বিভিন্ন ভিডিও ও internet ঘাটাঘাটি করে সময় নষ্ট করতে হবে না।
আচ্ছা তাইলে যদি বিম (ক্যাথড বিম) এর দৈর্ঘ্য যদি L হয় বা ধরো যে ক্যাথড রশ্মি যতটুকু দৈর্ঘ্য অতিক্রম করলো তার দৈর্ঘ্য L এবং এর বেগ V হলে আমরা সহজেই এটি কত সময়ে বিম অতিক্রম করবে পেয়ে যাবো। তাই না?

$$L=V_{cathod\;ray}T$$

$$T=\frac L{V_{{}_{cathod\;ray}}}$$

এবার সমীকরণ 1.1 এ মান গুলো বসানো যাক:

যেহেতু θ= O $$V_{0y}=V_0Sin\theta=V_0Sin0=0$$

সুতরাং $$S_y=0+\frac12a_yt^2$$

$$S_y=\frac12a_yt^2\\\;\;\;\;\;=\frac12\frac{qE}m\left(\frac LV\right)^2\\\;\;\;\;\;=\frac12\frac{qE}m\times\frac{L^2}{V^2}……..(1.2)$$

কিন্তু এখানে বেগ V কিন্তু একটা ঝামেলা করে রেখে গেলো, কারণ ক্যাথড রশ্মির বেগ V কত তুৃমি কেমনে জানবা?
এখানে একটা কথা বলে রাখা যাক তুমি চাইলে internet হতে এগুলো দেখতে পারো কিন্ত মজার বেপার তুমি ভিন্ন ভিন্ন জায়গায় বিভিন্ন মান দেখতে পাবা। তো এক্সপেরিমেন্টে আসলে যে রাশির মান যেমন ভাবে ব্যবহার করা হয়েছে সেই কন্ডিশনে V এর মান কেমন হবে তা বের করবো। আসলে জে.জে. থমসন তার পরীক্ষা চুম্বকক্ষেত্র ও তড়িৎ ক্ষেত্র উভয় ব্যবহার করেছিছেন। তো এর একটা ব্যবহার হলো বেগ বের করতে পারা, তো যদি কোন গতিশীল চার্জ এক্ষেত্রে বেগ V বলতে পারো চুম্বকক্ষেত্র B তে প্রবেশ করলে এর ওপর প্রযুক্ত বল: $$F_m=qVB$$
খেয়াল করো এখানে V কিন্তু cathod ray এর বেগ, কেন বলো তো? কারণ ঐ যে এটি অবেকগুলা ইলেক্ট্রনের সমন্বয়ে তৈরি।
তো চলো বেগ V বপর করা যাক:
ইলেক্ট্রনের ওপর যেহেতু তড়িৎ ক্ষেত্র ও চুম্বক ক্ষেত্রে উভয়েরই বল সমান হয় না, কিন্তু থমসন এমন ভাবে সেট করেছিলেন যে যাতে বল দুটি সমান মানের হয়। মানে Fm= Fe হয়।
সুতরাং,
$$F_m=F_e\\qVB=qE\\V=\frac EB$$

এবার মানগুলো সমীকরন 1.2 তে বসিয়ে পাই:

$$S_y=\frac12\frac{qE}{m_{electron}}\times\left(\frac{L^2}{V^2}\right)\\S_y=\frac12\frac{qE}m\times\left(\frac{L^2}{\displaystyle\frac{E^2}{B^2}}\right)\\S_y=\frac12\frac{qE}m\times\frac{L^2B^2}{E^2}\\\frac qm=\frac{2S_yE}{L^2B^2}$$

$$\frac qm=1.7\times10^{11}\;C/kg$$